The parallel axis theorem gives a relationship between the moment of inertia of a rigid body about an arbitrary axis and the moment of inertia about an axis passing through the center of mass and parallel to the former. The theorem states, “ The moment of inertia of a body about an arbitrary axis is equal to the sum of its moment of inertia about a parallel axis passing through its center of mass and the product of its mass and the square of the distance between the two axes .”
The parallel axis theorem is a convenient way to calculate the moment of inertia about any parallel axis since the moments of inertia few familiar objects can be found in tables.
Formula
Mathematically, the parallel axis theorem is written as
I O = I C + Md 2
I C is the moment of inertia about an axis passing through the center of mass.
I O is the moment of inertia about an arbitrary axis parallel to the axis passing through the center of mass.
M is the object’s mass.
d is the distance between the two parallel axes.
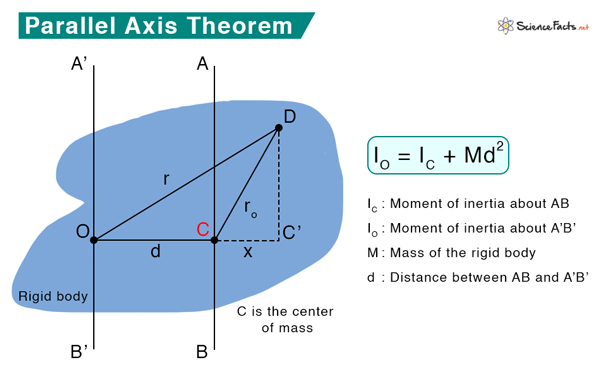
Derivation
In the image above, AB represents the axis passing through the center of mass C of the rigid body. A’B’ represents the axis passing through any arbitrary point D. A’B’ is at a distance d from AB. Consider an infinitesimal mass dm at point E.
We have the following quantities.
M: Mass of the body
dm: Infinitesimal mass of point D
I C : Moment of inertia about AB
I O : Moment of inertia about A’B’
h: Distance between the two parallel axes AB and A’B’
rₒ: Distance between points C and D
r: Distance between points O and D
x: Distance between points C and C’
The expressions for the moment of inertia are as follows:
Consider triangle OC’D.
(OD) 2 = (OC’) 2 + (C’D) 2
=> r 2 = (d + x) 2 + (C’D) 2
=> r 2 = (d + x) 2 + r o 2 – x 2
=> r 2 = d 2 + x 2 + 2dx + r o 2 – x 2
=> r 2 = r o 2 + d 2 + 2dx
Multiplying both sides by dm and integrating
The term ( \int x dm ) is zero since the integral of the moments of infinitesimal masses about the center of mass is always zero when the body is in equilibrium. Therefore, ( \int x dm = 0 ) , and we get,
I O = I C + Md 2
Thus, we have derived the parallel axis theorem.
When to Use Parallel Axis Theorem
The parallel axis theorem can determine the moment of inertia of a given rigid body about any axis. Let us look at a few examples.
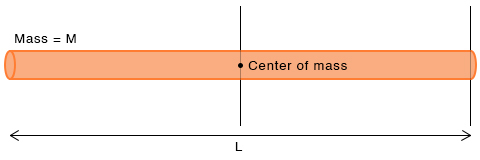
1. Uniform Rod
The moment of inertia I C of a thin rod of mass M and length L about an axis passing through its center is
Let us apply the parallel axis theorem to find the moment of inertia about its edge I O . We know that the edge is at a distance L/2 from the center; d = L/2.
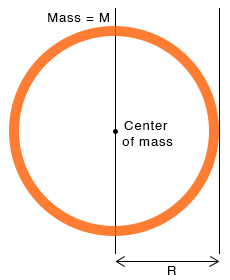
2. Ring
The moment of inertia I C of a ring of mass M and radius R about an axis passing through its center and perpendicular to the surface is
I C = MR 2
The edge is at a distance R from the center. Therefore, the moment of inertia about an axis tangential to the edge and perpendicular to the surface is
I O = MR 2 + MR 2
=> I O = 2MR 2
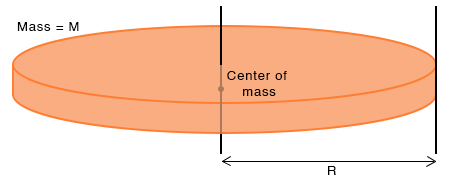
3. Disc
The moment of inertia I C of a disc of mass M and radius R about an axis passing through its center and perpendicular to the surface is
The edge is at a distance R from the center. Therefore, the moment of inertia about an axis tangential to the edge and perpendicular to the surface is
4. Sphere
The moment of inertia I C of a solid sphere of mass M and radius R about its central axis is
The surface is at a distance R from the center of the sphere. Therefore, the moment of inertia about an axis tangential to the surface is
Example Problems
Problem 1 . A body of mass 55 kg has a moment of inertia of 35 kg m 2 along an axis perpendicular to its center of gravity. What is its moment of inertia along a different axis parallel to and 40 cm from the center of mass axis?
Solution
Given
I C = 35 kg m 2 , M = 55 kg, and d = 40 cm = 0.4 m
From the parallel axis theorem,
I O = I C + Md 2
=> I O = 35 kg m 2 + 55 kg x (0.4 m) 2
=> I O = 43.8 kg m 2
Problem 2. Find the moment of inertia of a uniform rod with I C = 0.06 kg m 2 , L = 0.3 m, and mass = 1.50 kg about an axis perpendicular to the rod and passing through a point at 1/8 of the length of the rod.
Solution
Given I C = 0.06 kg m 2 , L = 0.3 m, and mass = 1.50 kg
From the parallel axis theorem
I O = I C + Md 2
Since the point is at a distance 1/8 of the length of the rod, we have
d = L/2 – L/8 = (3/8) L
=> d = (3/8) x 0.3 m = 0.1125 m
Therefore, the moment of inertia about an axis perpendicular to the rod and passing through the point in question is
I O = 0.06 kg m 2 + 1.50 kg x (0.1125 m) 2
=> I O = 0.079 kg m 2
- References Parallel Axis Theorem – Study.com Parallel Axis Theorem – Engineeringstatics.org Inertia Intro: Parallel Axis Theorem – Pressbooks.library.upei.ca Parallel Axis Theorem – Hyperphysics.phy-astr.gsu.edu Moments Of Inertia of Area: Parallel Axis Theorem – Engcourses-uofa.ca
Article was last reviewed on Friday, July 28, 2023



