Moment of inertia, also known as rotational inertia or angular mass, is a physical quantity that resists a rigid body’s rotational motion. It is analogous to mass in translational motion. It determines the torque required to rotate an object by a given angular acceleration. Moment of inertia does not restrict itself to a rigid body only. It also applies to a system of particles rotating about a common axis.
How to Calculate Moment of Inertia
Point Mass
For a point mass (single body), the moment of inertia formula is given by the product of mass and the square of the object’s perpendicular distance from the axis of rotation.
Where
I is the moment of inertia
m is the mass
r is the perpendicular distance from the axis of rotation
System of Particles
Suppose n particles of masses m 1 , m 2 , …, m n rotate about a common axis at perpendicular distances r 1 , r 2 , …, r n from the axis. Then the moment of inertia of the system is
The moment of inertia of a system of particles is the sum of the moments of inertia of the individual particles taken about a common axis.
Units and Dimensions
The SI unit of moment of inertia is kgˑm 2 , and the cgs unit is gˑcm 2 . The dimension is [M L 2 T 0 ].
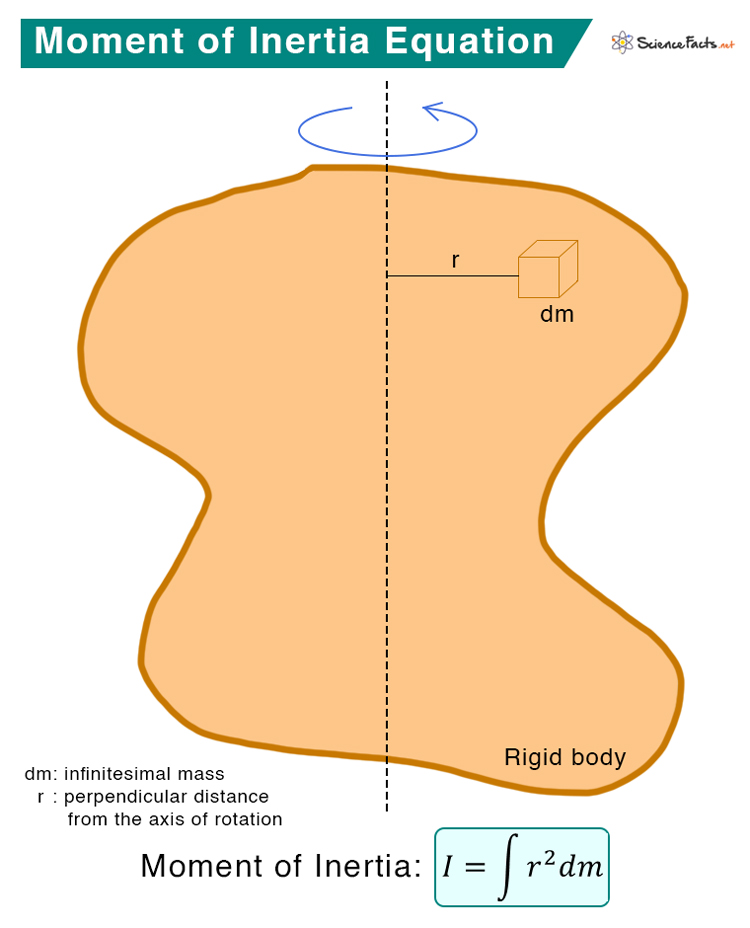
Integral Moment of Inertia
For a continuous mass distribution, the integral form of moment of inertia is given by
Where dm is the instantaneous mass.
The above equation can also be written in terms of density ρ and instantaneous volume dV as follows.
Moment of Inertia Formula
Moment of Inertia Table
Several everyday objects, such as rotating disks, cylinders, and spheres, have well-defined moment of inertia formulas. A chart consisting of the different formulas is listed in the table below. Here M represents mass, R represents radius, and L represents the length.

Moment of Inertia
Moment of Inertia and Rotational Kinematics
The moment of inertia of a rotating object about a fixed axis is useful in calculating a few key quantities in rotational motion. Newton’s second law for rotation gives a relationship between torque, moment of inertia, and angular acceleration. According to this law,
Where
τ is the applied torque
I is the moment of inertia
α is the angular acceleration
The relationship between moment of inertia and rotational kinetic energy is given by
And with angular momentum, the equation is
Where
K is the rotational kinetic energy
L is the angular momentum
ω is the angular velocity
Factors Affecting Moment of Inertia
The moment of inertia depends upon
The shape of the object
Mass distribution or density
Location of the axis of rotation
References Moment of Inertia – Hyperphysics.phy-astr.gsu.edu Rotational Inertia – Khanacademy.org Moment of Inertia – Isaacphysics.org What Is Moment of Inertia in Physics? – Thoughtco.com Center of Mass; Moment of Inertia – Feynmanlectures.caltech.edu Calculating Moment of Inertia – Phys.libretexts.org
Article was last reviewed on Wednesday, August 2, 2023



